SEDUVAN::PASCAL

:: PASCAL :: ТЕОРИЯ

Лекция 9

Алгоритмы поиска и сортировки массива.

1. Поиск элемента массива с максимальным значением.

Пусть значения элементов линейного массива x сформированы. Требуется среди чисел x[1], x[2], …, x[n] найти такое, что

x[j] = max(x[1], x[2], …, x[n]).

Если в задаче требуется найти порядковый номер этого элемента, то значит необходимо найти еще и значение индекса j.

Основная идея алгоритма состоит в том, что переменной max присваивается значение любого элемента массива (чаще всего первого по порядку). В случае нахождения порядкового номера переменной ind присваивается значение индекса этого элемента (т.е. 1).

Далее просматриваются все элементы массива, значения которых сравниваются со значением переменной max. Если окажется, что значение какого-либо элемента массива превосходит значение переменной max, то переменная max меняет свое значение на значение большего элемента. В случае отыскания порядкового номера переменная ind запоминает значение индекса большего элемента.

Если поиск наибольшего элемента идет в двумерном массиве, то необходимо просматривать поочередно все элементы каждой из строк. Для этого можно воспользоваться вложенными циклами:

max:=x[1,1];

indstr:=1;

indcol:=1;

for i:=1 to n do

for j:=1 to m do

if x[i,j] > max then

begin

max:=x[i,j];

indstr:=i;

indcol:=j;

end;

2. Методы сортировки массивов.

Задача сортировки (упорядочения) элементов массива в соответствии с их значением – классическая задача, исследование которой началось еще с момента появления первых ЭВМ. Создано много различных алгоритмов сортировки, однако задача разработки такого метода сортировки, который был бы эффективен для массивов с любым количеством элементов, т.е. упорядочивал массив за наименьшее количество времени при минимальном объеме затрачиваемой памяти, не потеряла своей актуальности. В последнее время появилось достаточно много эффективных алгоритмов сортировки, которые базируются на принципах рекурсии, динамического программирования.

Рассмотрим несколько типов сортировки.

Договоримся для удобства, что в каждой задаче требуется упорядочить массив по возрастанию значений его элементов.

1. Метод «пузырька»

Идея метода:

весь массив просматривается несколько раз, причем при каждом просмотре сравниваются значения двух соседних элементов. Если эти значения следуют не в порядке возрастания, то производится их перестановка. Так происходит до тех пор, пока не будет сделано ни одной перестановки.

Этот метод называют «пузырьковой сортировкой» потому, что меньшие значения элементов массива постепенно «всплывают», как легкие пузырьки воздуха в воде, и перемещаются в начало массива, в то время, как б'ольшие значения «оседают на дно», т.е. перемещаются в конец массива.

  procedure float (k:integer; var t:mass);
   var i,j,h: integer;
   begin
      for i:=2 to k do
         for j:=k downto i do
         if t[j]<t[j-1] then
         begin
            h:=t[j];
            t[j]:=t[j-1];
            t[j-1]:=h;
         end;
   end;

2. Метод простых обменов.

Идея метода:

весь массив просматривается несколько раз и при каждом просмотре ищется минимальный по значению элемент, который меняется местами с первым, вторым, третьим, …, предпоследним элементов массива и исключается из дальнейшего рассмотрения.

procedure obmen (k:integer; var t: mass);

var i, j, min, ind, h: integer;

begin

for i:=1 to k-1 do

begin

min:=t[i];

ind:=i;

for j:=i+1 to k do

if t[j] < min then

begin

min:=t[j];

ind:=j;

end;

h:=t[i];

t[i]:=t[ind];

t[ind]:=h;

end;

3. Метод вставки и сдвига.

Идея метода:

делается предположение, что первые q элементов массива упорядочены, и если q+1-ый элемент меньше, чем какой-либо из первых q, то он записывается на свое место среди упорядоченных, при этом «хвост» массива «сдвигается» к концу.

procedure vstavka (k:integer; var t:mass);

var i,j: integer;

procedure sdvig (p,g:integer; var tt:mass);

var f,h:integer;

begin

f:=tt[p];

for h:=p downto g+1 do

tt[h]:=tt[h-1];

tt[g]:=f;

end;

begin

for i:=2 to k do

for j:=1 to i-1 do

if t[i]<t[j] then sdvig(i,j,t);

end;

4. Метод быстрой сортировки (QuickSort).

Автор алгоритма быстрой сортировки лауреат премии Тьюринга за 1980 г. профессор вычислительной математики Оксфордского университета в Англии Чарльз Хоар сказал:

«… Я написал программу, нескромно названную «быстрая сортировка», которая легла в основу моей карьеры ученого в области компьютеров. Следует отдать должное гению разработчиков Лгола-60 за то, что они включили в свой язык рекурсию и дали мне тем самым возможность элегантно описать мое изобретение».

В основу алгоритма быстрой сортировки положена идея перестановок на большие расстояния.

Идея метода:

выбирается наугад элемент массива x[i] и массив просматривается слева до тех пор, пока не будет найден такой x[j], что x[j]>x[i]. После этого просматриваем массив справа до тех пор, пока не будет найден такой x[g], что x[g]<x[i]. Меняем местами x[j] и x[g]. Процесс продолжается, пока мы не дойдем приблизительно до середины массива. В результате в левой половине массива окажутся элементы меньшие или равные x[i], а в правой – большие или равные x[i]. Полученный массив далее сортируем следующим образом:

разделяем каждую из полученных частей;

разделяем каждую часть частей и т.д. до тех пор, пока в каждой части останется по одному элементу (очевидно, что в этом случае совпадают индексы начала и конца просмотра массива).

procedure quick_sort(le,ri:integer; var x:mass);

var i,j,t,z: integer;

begin

i:=le; j:=ri;

t:=x[(le+ri) div 2];

repeat

while x[i]<t do i:=i+1;

while x[j]>t do j:=j-1;

if i<=j then

begin

z:=x[i];

x[i]:=x[j];

x[j]:=z;

i:=i+1;

j:=j-1;

end

until i>j;

if le<j then quick_sort(le,j,x);

if i<ri then quick_sort(i,ri,x);

end;

5. Метод пирамидальной сортировки.

Все методы сортировок основаны на многократных просмотрах массива и выполнении определенных операций над его элементами. Как можно улучшить какой-либо из конкретных алгоритмов? По-видимому, путь таков: за каждый просмотр всего массива или его части получать как можно больше информации. Одна из возможностей на этом пути открывается при представлении сортируемого массива в виде нелинейной структуры типа двоичного (бинарного) дерева.

Идея метода:

метод состоит из нескольких этапов:

1) построение дерева выбора с нахождением его корня, для чего все элементы сравниваются попарно и больший «поднимается» вверх, где сравнивается с другим б'ольшим и т.д. В результате будет найден корень дерева – максимальный элемент массива;

2) спуск вдоль пути, отмеченного наибольшим элементом, и исключение его путем замены либо на «дырку» (пустой элемент), либо на элемент из соседней ветви в промежуточных вершинах.

Пирамида – это последовательность из n элементов такая, что каждый элемент с номером i (i=1..n/2) больше либо равен элементов с номерами 2i и 2i+1, называемых потомками данного элемента. Заметим, что элементы с номерами от n/2+1 до n уже образуют пирамиду, т.к. не существует двух индексов h и g таких, что h=2g и h=2g+1.

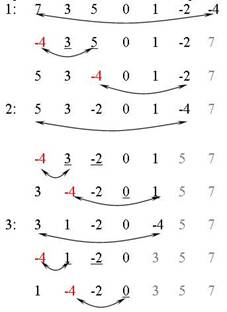
Построим пирамиду для данного массива:

- элементы 3,1,-2,5 образуют пирамиду;

- берем первый элемент, сравниваем его с двумя потомками и если он окажется меньше какого-либо из них, то меняем их местами (в случае, если претендентов на обмен два, выбираем наибольший из них);

- «просеивание» каждого элемента из левой части массива продолжается до тех пор, пока для каждого из элементов массива не выполнится требование пирамиды.

В текущей пирамиде начальный элемент не меньше остальных. Обменяем значениями концевые (начальный и конечный) элементы массива и укоротим пирамиду справа на один элемент. Полученная последовательность уже может и не быть пирамидой. Применим в ней к каждому элементы процесс «просеивания». В результате n шагов просеивания все элементы пирамиды будут упорядочены.

procedure shift(le,ri:integer; var x:mass);

var q,p,z:integer;
begin
q:=2*le;
p:=q+1;
if q<=ri then
begin
if p<=ri then
if x[p]>x[q] then q:=p;
if x[le]<x[q] then
begin
z:=x[le];
x[le]:=x[q];
x[q]:=z;
shift(q,ri,x);
end;
end;
end;

Процедура просеивает в массиве x элемент от позиции le до позиции ri. При этом, если значение элемента x[le] не меньше значений в позициях-потомках, то вычисления прекращаются. В противном случае значениями обмениваются x[le] и потомок с наибольшим значением.

procedure build(q1,ri1:integer; var x1:mass);
begin
shift(q1,ri1,x1);
if q1>1 then build(q1-1,ri1,x1);
end;
Процедура строит на участке [1,ri1] в массиве x1 пирамиду, считая, что на участке [q1+1, ri1] пирамида уже построена.
procedure sort(rigth:integer; var xx:mass);
var h:integer;
begin
h:=xx[1];
xx[1]:=xx[rigth];
xx[rigth]:=h;
shift(1,rigth-1,xx);
if rigth>2 then sort(rigth-1,xx);
end;

Процедура на участке [1, right] в массиве xx сортирует по неубыванию заранее построенную пирамиду.

В случае использования указанных процедур главная программа может выглядеть следующим образом:

Begin

clrscr;

randomize;

gen_1(-20,20,15,m);

vivod_1(1,1,5,15,m);

left:=n div 2;

if n>1 then

begin

build(left,n,m);

sort(n,m);

end;

vivod_1(1,5,5,15,m);

readln;

End.
В заключение отметим, что рассмотренный нами метод бинарной пирамидальной сортировки может быть обобщен до метода s-арной пирамидальной сортировки, при котором для каждого элемента массива рассматривается ровно по s потомков и соответственно строятся s-арное дерево и s-арная пирамида.

(с)2005-2006 Web studio SEDUVAN